Post
Let's estimate the Grand Authentic Symbol tax in advance (applied up to level 2)
Some calculations, 3-line summary at the end
//
Hello
I was browsing 꺼라위키 at dawn and
I saw that the Tenebris Symbol price had gone up.
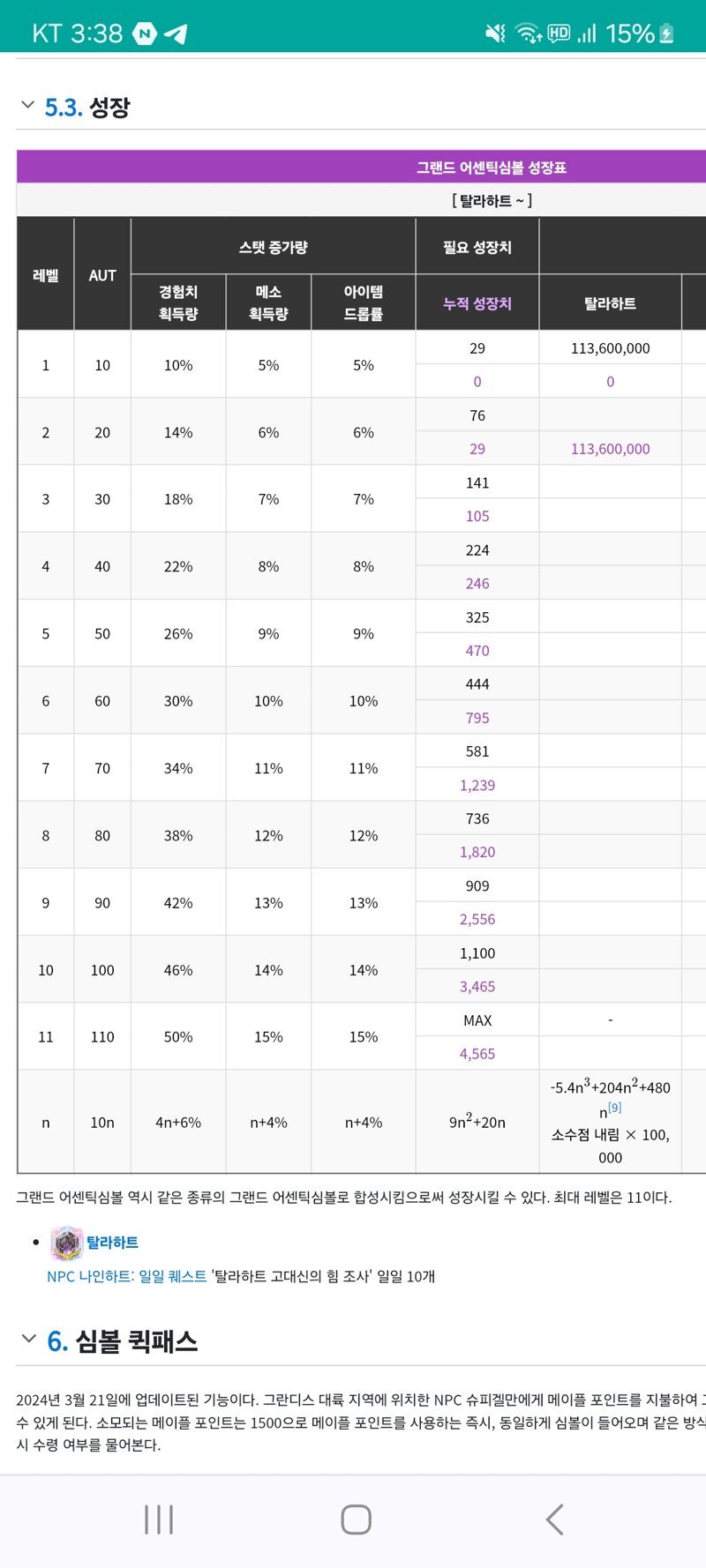
But the formula applied, int { -5.4n^3+204n^2+480n } × 100,000, and the tax written there is
Based on level 1, when n=1, it's 67,800,000 mesos, which is different from the 113,600,000 mesos in the picture,
Considering that there are no comparison groups for the level 2 symbol price or other Grand Authentic Symbols yet, I tried to correct the formula and estimate the amount.
The estimation in this post may be incorrect as the prices for level 2 and beyond are revealed in future test servers and live servers.
Main point.
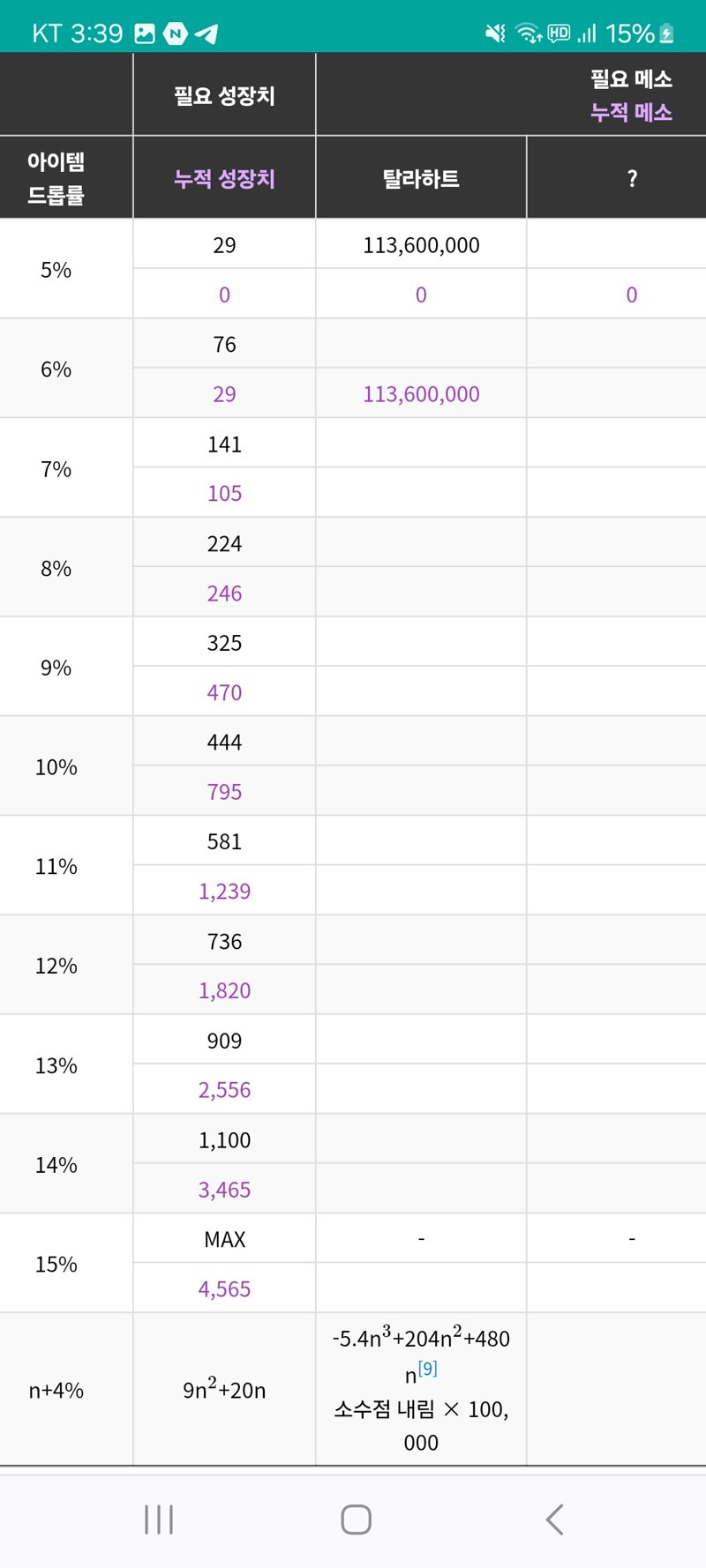
How is 113,600,000 mesos calculated?
The existing Authentic Symbol price calculation formula is
Required growth × 1.8 (constant) × {(region constant + 6) - (level - 1)÷3}.
Required growth is the number of symbols required to level up for each level,
It is represented as 9n^2+20n. (n is the level of the symbol)
The region constant increases by 1 each time you pass an Authentic Force region. (ex Arteria = 5, Carsion = 6)
However, if you substitute the region constant of Tenebris, assumed to be 7, into the formula, it doesn't match, so it is determined that the constant of 1.8 has increased.
If we set f(n) = (9n^2+20n) × constant k × (40-n) / 3,
When n=1, f(1) = 29 × constant k × 13 = 1136+m (0≤m<1)
3.013... < k < 3.015...
The constant means it's between 3.013 and 3.015, but it's not pretty to set it as a value.
We recalculated assuming the region constant has also changed.
If we set g(n) = (9n^2+20n) × constant k × constant p,
When n=1, g(1) = 29 × constant k × constant p = 1136+m (0≤m<1)
39.1724... < k × p < 39.2068...
Praying to Nexon, who set the constant k of the existing Arcane Symbol to 2 and the constant k of the Authentic Symbol to 1.8,
Taking into account that the existing region constant was attached in the form of {(region constant + 6) - (level - 1)÷3},
The number of cases where p is an integer
We created ordered pairs with k in 0.1 increments and found the most appropriate p.
(1.4,27.98...,28.00...)
(2.8,13.99...,14.00...) ...☆
(4.9,07.99...,08.00...)
We found 14 as the value closest to the existing region constant.
Therefore, the constant k can be said to be 2.8,
If we rewrite the formula,
G(n) = 9n^2+20n (required growth) × 2.8 (constant) × {(region constant + 6) - (level - 1) ÷3 } (However, the Tenebris region constant is 8)
It can be written as.
This can be expressed as -25.2n^3+1027.6n^2+2408n (excluding decimals and multiplying by 100,000)
If we calculate the amount up to level 11 using this,
Level 1 113,600,000
Level 2 290,800,000
Level 3 526,400,000
Level 4 815,300,000
Level 5 1,152,600,000
Level 6 1,533,200,000
Level 7 1,952,100,000
Level 8 2,404,200,000
Level 9 2,884,500,000
Level 10 3,388,000,000 mesos.
Congratulations.
You (including me) have to pay 15,060,700,000 mesos in taxes.
Take it or leave it
//
Hello
I was browsing 꺼라위키 at dawn and
I saw that the Tenebris Symbol price had gone up.
But the formula applied, int { -5.4n^3+204n^2+480n } × 100,000, and the tax written there is
Based on level 1, when n=1, it's 67,800,000 mesos, which is different from the 113,600,000 mesos in the picture,
Considering that there are no comparison groups for the level 2 symbol price or other Grand Authentic Symbols yet, I tried to correct the formula and estimate the amount.
The estimation in this post may be incorrect as the prices for level 2 and beyond are revealed in future test servers and live servers.
Main point.
How is 113,600,000 mesos calculated?
The existing Authentic Symbol price calculation formula is
Required growth × 1.8 (constant) × {(region constant + 6) - (level - 1)÷3}.
Required growth is the number of symbols required to level up for each level,
It is represented as 9n^2+20n. (n is the level of the symbol)
The region constant increases by 1 each time you pass an Authentic Force region. (ex Arteria = 5, Carsion = 6)
However, if you substitute the region constant of Tenebris, assumed to be 7, into the formula, it doesn't match, so it is determined that the constant of 1.8 has increased.
If we set f(n) = (9n^2+20n) × constant k × (40-n) / 3,
When n=1, f(1) = 29 × constant k × 13 = 1136+m (0≤m<1)
3.013... < k < 3.015...
The constant means it's between 3.013 and 3.015, but it's not pretty to set it as a value.
We recalculated assuming the region constant has also changed.
If we set g(n) = (9n^2+20n) × constant k × constant p,
When n=1, g(1) = 29 × constant k × constant p = 1136+m (0≤m<1)
39.1724... < k × p < 39.2068...
Praying to Nexon, who set the constant k of the existing Arcane Symbol to 2 and the constant k of the Authentic Symbol to 1.8,
Taking into account that the existing region constant was attached in the form of {(region constant + 6) - (level - 1)÷3},
The number of cases where p is an integer
We created ordered pairs with k in 0.1 increments and found the most appropriate p.
(1.4,27.98...,28.00...)
(2.8,13.99...,14.00...) ...☆
(4.9,07.99...,08.00...)
We found 14 as the value closest to the existing region constant.
Therefore, the constant k can be said to be 2.8,
If we rewrite the formula,
G(n) = 9n^2+20n (required growth) × 2.8 (constant) × {(region constant + 6) - (level - 1) ÷3 } (However, the Tenebris region constant is 8)
It can be written as.
This can be expressed as -25.2n^3+1027.6n^2+2408n (excluding decimals and multiplying by 100,000)
If we calculate the amount up to level 11 using this,
Level 1 113,600,000
Level 2 290,800,000
Level 3 526,400,000
Level 4 815,300,000
Level 5 1,152,600,000
Level 6 1,533,200,000
Level 7 1,952,100,000
Level 8 2,404,200,000
Level 9 2,884,500,000
Level 10 3,388,000,000 mesos.
Congratulations.
You (including me) have to pay 15,060,700,000 mesos in taxes.
Take it or leave it
============
Added September 15, 2024
The amount from level 2 -> level 3 has been confirmed to be 293,300,000.
All estimated formulas are incorrect,
When setting the region constant to 21.78 based on the basic constant of 1.8,
Level 1113,600,000
Level 2293,300,000
Level 3535,800,000
4레벨837,800,000
5레벨1,196,100,000
6레벨1,607,400,000
7레벨2,068,500,000
8레벨2,576,200,000
9레벨3,127,300,000
10레벨3,718,400,000
Total16,075,026,000
This is also not certain until the level-up cost for level 3 is confirmed.
메이플스토리 인벤 팁과노하우레키어드렌
2024-09-06
Your gaming prime time starts now!Sign-in to Vortex Gaming, receive gaming news and engaging contents!